1. Synopsis
One of the major headaches of using complex numbers in olympiad geometry problems is dealing with square roots. In particular, it is nontrivial to express the incenter of a triangle inscribed in the unit circle in terms of its vertices.
The following lemma is the standard way to set up the arc midpoints of a triangle. It appears for example as part (a) of Lemma 6.23.
Theorem 1 (Arc midpoint setup for a triangle)
Let be a triangle with circumcircle
and let
,
,
denote the arc midpoints of
opposite
,
opposite
,
opposite
.
Suppose we view as the unit circle in the complex plane. Then there exist complex numbers
,
,
such that
,
,
, and
Theorem 1 is often used in combination with the following lemma, which lets one assign the incenter the coordinates in the above notation.
Lemma 2 (The incenter is the orthocenter of opposite arc midpoints)
Let be a triangle with circumcircle
and let
,
,
denote the arc midpoints of
opposite
,
opposite
,
opposite
. Then the incenter of
coincides with the orthocenter of
.
Unfortunately, the proof of Theorem 1 in my textbook is wrong, and I cannot find a proof online (though I hear that Lemmas in Olympiad Geometry has a proof). So in this post I will give a correct proof of Theorem 1, which will hopefully also explain the mysterious introduction of the minus signs in the theorem statement. In addition I will give a version of the theorem valid for quadrilaterals.
2. A Word of Warning
I should at once warn the reader that Theorem 1 is an existence result, and thus must be applied carefully.
To see why this matters, consider the following problem, which appeared as problem 1 of the 2016 JMO.
Example 3 (JMO 2016, by Zuming feng)
The isosceles triangle , with
, is inscribed in the circle
. Let
be a variable point on the arc
that does not contain
, and let
and
denote the incenters of triangles
and
, respectively. Prove that as
varies, the circumcircle of triangle
passes through a fixed point.
By experimenting with the diagram, it is not hard to guess that the correct fixed point is the midpoint of arc , as seen in the figure below. One might be tempted to write
,
,
,
and assert the two incenters are
and
, and that the fixed point is
.
This is a mistake! If one applies Theorem 1 twice, then the choices of “square roots” of the common vertices and
may not be compatible. In fact, they cannot be compatible, because the arc midpoint of
opposite
is different from the arc midpoint of
opposite
.
In fact, I claim this is not a minor issue that one can work around. This is because the claim that the circumcircle of passes through the midpoint of arc
is false if
lies on the arc on the same side as
! In that case it actually passes through
instead. Thus the truth of the problem really depends on the fact that the quadrilateral
is convex, and any attempt with complex numbers must take this into account to have a chance of working.
3. Proof of the theorem for triangles
Fix now, so we require
,
,
. There are
choices of square roots
,
,
we can take (differing by a sign); we wish to show one of them works.
We pick an arbitrary choice for first. Then, of the two choices of
, we pick the one such that
. Similarly, for the two choices of
, we pick the one such that
. Our goal is to show that under these conditions, we have
again.
The main trick is to now consider the arc midpoint , which we denote by
. It is easy to see that:
Lemma 4 (The isosceles trapezoid trick)
We have (both are perpendicular to the
bisector). Thus
is an isosceles trapezoid, and so
.
Thus, we have
Thus
as desired.
From this we can see why the minus signs are necessary.
4. A version for quadrilaterals
We now return to the setting of a convex quadrilateral that we encountered in Example 3. Suppose we preserve the variables
,
,
that we were given from Theorem 1, but now add a fourth complex number
with
. How are the new arc midpoints determined? The following theorem answers this question.
Theorem 6 ( setup)
Let be a convex quadrilateral inscribed in the unit circle of the complex plane. Then we can choose complex numbers
,
,
,
such that
,
,
,
and:
- The opposite arc midpoints
,
,
of triangle
are given by
,
,
, as before.
- The midpoint of arc
not including
or
is given by
.
- The midpoint of arc
not including
or
is given by
.
- The midpoint of arc
is
and the midpoint of arc
is
.
This setup is summarized in the following figure.
Note that unlike Theorem 1, the four arcs cut out by the sides of do not all have the same sign (I chose
to have coordinates
). This asymmetry is inevitable (see if you can understand why from the proof below).
Proof: We select ,
,
with Theorem 1. Now, pick a choice of
such that
is the arc midpoint of
not containing
and
. Then the arc midpoint of
not containing
or
is given by
On the other hand, the calculation of for the midpoint of
follows by applying Lemma 4 again. (applied to triangle
). The midpoint of
is computed similarly.
In other problems, the four vertices of the quadrilateral may play more symmetric roles and in that case it may be desirable to pick a setup in which the four vertices are labeled in order. By relabeling the letters in Theorem 6 one can prove the following alternate formulation.
Corollary 7
Let be a convex quadrilateral inscribed in the unit circle of the complex plane. Then we can choose complex numbers
,
,
,
such that
,
,
,
and:
- The midpoints of
,
,
,
cut out by the sides of
are
,
,
,
.
- The midpoints of
and
are
and
.
- The midpoints of
and
are
and
.
To test the newfound theorem, here is a cute easy application.
Example 8 (Japanese theorem for cyclic quadrilaterals)
In a cyclic quadrilateral , the incenters of
,
,
,
are the vertices of a rectangle.






Here’s my preferred way to think about this: let $A_1A_2\dots A_n$ be a cyclic $n$-gon on the unit circle with $n\geq3$, and let $B_{1,2},B_{2,3},\dots,B_{n,1}$ be the midpoints of the $n$ arcs partitioning the circle.
Key Observation: if $A_1,A_2,\dots,A_n$ go counterclockwise around the circle, then the product $\prod_i B_{i,i+1} A_i^{-1}$ is $\exp(i\pi) = -1$, because the sum of the corresponding arcs is precisely half the circumference.
So, if $a_1$ is an arbitrary square root of $A_1$, then there is a **unique** square root $a_2$ of $A_2$ such that $B_{1,2} = -a_1a_2$: namely, $a_2 = -B_{1,2} a_1^{-1}$ works! Continuing in this manner uniquely specifies all $a_i$. The catch is, the choice is consistent if and only if $n$ is odd: we require $(-1)^n$ to be consistent with $-1$ from the Key Observation.
The case $n$ is even (e.g. quadrilateral as you discuss) is similar, except we can no longer take all the signs in the $B_{i,i+1} = \pm a_ia_{i+1}$ to be $-1$. An odd number of the signs must be $+1$ instead.
LikeLiked by 3 people
In the explanation for the cyclic inductive construction, I should have elaborated that the terms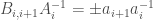 form a cyclic telescoping product (I only mentioned the sign issues). In any case, an example where I needed to think through this carefully was http://artofproblemsolving.com/community/c6h404946p2271784
form a cyclic telescoping product (I only mentioned the sign issues). In any case, an example where I needed to think through this carefully was http://artofproblemsolving.com/community/c6h404946p2271784
(Sorry I forgot about WordPress math in the previous comment, and I can’t seem to edit.)
LikeLiked by 1 person
No comments on the post, but a question: what do you use for writing WordPress math? I am struggling with open-source solutions. Thank you in advance!
LikeLiked by 1 person
I use https://lucatrevisan.wordpress.com/latex-to-wordpress/ :)
LikeLiked by 1 person
I’ve been attempting exercise 5 for about half an hour now. I can’t seem to understand why *all* the minus signs would be necessary as interpretively stated on the line before the exercise. Is it not more like – having the three minus signs allows to have symmetric expressions for the formulation of the theorem but we could also just get away with using one?
LikeLike
You can indeed just use one minus sign and it’s fine too. But not zero.
LikeLike