Joyal’s Proof of Cayley’s Tree Formula

Posted on by Evan Chen (陳誼廷)

I wanted to quickly write this proof up, complete with pictures, so that I won’t forget it again. In this post I’ll give a combinatorial proof (due to Joyal) of the following:

Theorem 1 (Cayley’s Formula)

The number of trees on {n} labelled vertices is {n^{n-2}}.

Proof: We are going to construct a bijection between

  • Functions {\{1, 2, \dots, n\} \rightarrow \{1, 2, \dots, n\}} (of which there are {n^n}) and
  • Trees on {\{1, 2, \dots, n\}} with two distinguished nodes {A} and {B} (possibly {A=B}).

This will imply the answer.

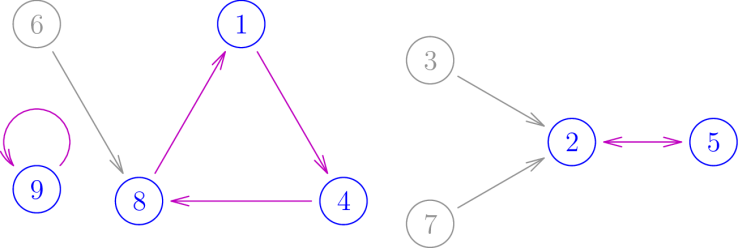
Let’s look at the first piece of data. We can visualize it as {n} points floating around, each with an arrow going out of it pointing to another point, but possibly with many other arrows coming into it. Such a structure is apparently called a directed pseudoforest. Here is an example when {n = 9}.

cayley-pseudoforest

You’ll notice that in each component, some of the points lie in a cycle and others do not. I’ve colored the former type of points blue, and the corresponding arrows magenta.

Thus a directed pseudoforest can also be specified by

  • a choice of some vertices to be in cycles (blue vertices),
  • a permutation on the blue vertices (magenta arrows), and
  • attachments of trees to the blue vertices (grey vertices and arrows).

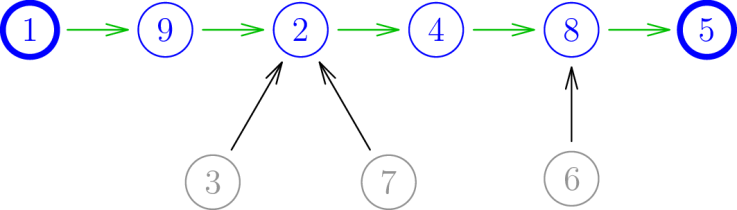
Now suppose we take the same information, but replace the permutation on the blue vertices with a total ordering instead (of course there are an equal number of these). Then we can string the blue vertices together as shown below, where the green arrows denote the selected total ordering (in this case {1 < 9 < 2 < 4 < 8 < 5}):

cayley-tree

This is exactly the data of a tree on the {n} vertices with two distinguished vertices, the first and last in the chain of green (which could possibly coincide). \Box

Published by Evan Chen (陳誼廷)

I am a math olympiad coach and a PhD student at MIT.

5 thoughts on “Joyal’s Proof of Cayley’s Tree Formula”

  1. Hey you stupid fucking mathematician cunts would it fucking kill you to write out a goddamn sentence, with actual fucking words, once in a while explaining what the fuck it even is that you just fucking did or what the fuck I’m supposed to actually do with your stupid fucking abstract mathematical objects? I know you have some sick fetish/obsession with trying to explain everything with just numbers and symbols and using the least amount of words possible because you were probably such a fucking socially awkward weirdo your whole life that now you need to try and prove you’re better than anyone at all making your fucking ideas unnecessarily obtuse and inaccessible to anyone but your snide little mathematician friends, but the only reason we keep you on the payroll is to come up with tools for us to use to solve real problems. Sure we let you dick around with your insanely nonsensical 97 dimensional semicuspidal manifolds or your hyperbolic triangles without embedded eigenvalues or whatever the fuck it is you assholes are doing all day. But that’s just to keep you little shits busy so you don’t bother the rest of us with your fucking bullshit periodic approximations of irrational pseudo-rotations using pseudoholomorphic curves. Jesus Fucking Christ. All I’m asking for is ONE (maybe 2) sentences explaining what the fuck this shit even represents. You can blame it on me. Tell your math buddies I snuck it and wrote ‘words’ while you weren’t looking. Just please, for the love of god, tell the rest of us what you are doing and what you want us to do.

    Like

    1. They’re drawn using Asymptote (https://web.evanchen.cc/asyguide.html). The source code for that particular diagram was:

      size(11cm);

      real R = 0.2;
      void to(pair A, pair B, pen p = defaultpen) {
      draw((A+R*dir(B-A))–(B+R*dir(A-B)), p, Arrow(SimpleHead), Margins);
      }
      pair vx(Label L, pair A, pen p = defaultpen) {
      draw(circle(A,R), p); label(L, A, (0,0), p);
      return A;
      }

      pen bl = blue;
      pen gr = grey;
      pen ma = heavymagenta;

      pair A1 = vx(“$1$”, dir( 90) – 2 * dir(0), bl);
      pair A4 = vx(“$4$”, dir(330) – 2 * dir(0), bl);
      pair A8 = vx(“$8$”, dir(210) – 2 * dir(0), bl);
      pair A6 = vx(“$6$”, A1 + A8 – A4, gr);

      to(A1, A4, ma);
      to(A4, A8, ma);
      to(A8, A1, ma);
      to(A6, A8, gr);

      pair A3 = vx(“$3$”, 0.8*dir(120), gr);
      pair A7 = vx(“$7$”, 0.8*dir(240), gr);
      pair A2 = vx(“$2$”, 0.8*dir(0), bl);
      pair A5 = vx(“$5$”, A2+1.2*dir(0), bl);
      to(A3, A2, gr);
      to(A7, A2, gr);
      to(A2, A5, ma);
      to(A5, A2, ma);

      pair A9 = vx(“$9$”, A6+1.4*dir(270), bl);
      draw(arc(A9+2*R*dir(90), 1.4*R, -60, 240), ma, Arrow(SimpleHead), Margins);

      Like

    2. and for the second figure:

      size(9cm);

      real R = 0.2;
      void to(pair A, pair B, pen p = defaultpen) {
      draw((A+R*dir(B-A))–(B+R*dir(A-B)), p, Arrow(SimpleHead), Margins);
      }
      pair vx(Label L, pair A, pen p = defaultpen) {
      draw(circle(A,R), p); label(L, A, (0,0), p);
      return A;
      }

      pen bl = blue;
      pen gr = grey;
      pen hg = heavygreen;

      pair B1 = vx(“$1$”, (-2,0), bl+2);
      pair B9 = vx(“$9$”, (-1,0), bl);
      pair B2 = vx(“$2$”, ( 0,0), bl);
      pair B4 = vx(“$4$”, ( 1,0), bl);
      pair B8 = vx(“$8$”, ( 2,0), bl);
      pair B5 = vx(“$5$”, ( 3,0), bl+2);
      to(B1, B9, hg);
      to(B9, B2, hg);
      to(B2, B4, hg);
      to(B4, B8, hg);
      to(B8, B5, hg);

      pair B3 = vx(“$3$”, B2+1.3*dir(240), gr);
      pair B7 = vx(“$7$”, B2+1.3*dir(-60), gr);
      pair B6 = vx(“$6$”, B8+1.1dir(270), gr);
      to(B3, B2);
      to(B7, B2);
      to(B6, B8);

      Like

Leave a comment